On building a verifiable log, part 1: core ideas

Building a system able to make evident any non-authorized modification to some stored data is not an easy task. As will be discussed, traditional and experimental approaches tend to lack fundamental performance under write-heavy workloads due to concurrency limitations. In this series of articles, we will share our experience building a possible solution from scratch. We will explore the kind of data structures available and the process we followed for selecting the more suitable ones. But also, we will discuss the key decisions concerning every database system, like storage, consistency models, replication, etc. All of our choices are reflected in a project we have named QED[1].

In this part (1) of the series, we introduce in detail the problem to solve and discuss the academic approaches and intuitions that led us to an appropriate data structure: one capable of enabling auditing for correctness while remaining efficient.

Introduction

We could say that we are preserving the integrity of a data collection if we can assure that such data has not been modified by an unknown user in a non-authorized manner. This is an essential feature within the scope of many activities that collect critical user information, like banking or health services. We can imagine multiple scenarios where either a malicious attacker or a privileged insider can perform undetected activities modifying the previously stored data.

Organizations tend to use general and widely-known database systems to store their data and try to limit the kind of operations users can perform on them by using authentication and access control mechanisms. A usual strategy to secure a system is to reduce its vulnerability surface. This involves implementing server hardening in order to protect the system against well-known attacks. Or even using trusted hardware to accommodate critical applications. However, these mechanisms may be insufficient to completely ensure the integrity of the data and, in the end, the data owner would need to make an act of trust on the proper configuration and operation of the server by privileged users. When a breach happens, forensic analysis is the only tool they can rely on, which is reactive in nature.

Regarding the relationship with the customer, that insufficiency forces organizations to try to keep a state of confidence with respect to the integrity of the data they collect. But, in the end, an annoyed or even a malicious customer could demand proofs or claim spurious statements about data corruption and take legal action.

These reasons motivate the exploration of a verification mechanism to data integrity.

A matter of auditing

It is common practice to capture the variety of threats, abuses and patterns a system is exposed to, and the techniques needed to prevent them, in what is called an attack model. An attack model is useful to help us think like an attacker. While the majority of security approaches assume a relaxed notion of an attacker, the problem we are dealing with demands a more stringent one: that is, an insider with full access and knowledge over the server where data resides, including the capability of managing all cryptographic elements. This means that the server is completely untrusted. We can deduce that this attack model, focused on insiders, encompasses an external attack model.

The main consequence of assuming this insider attack model—given that it is impractical to prevent the alteration of digital records—is that we shift our focus from prevention to detection. Enabling tampering detection requires storing such records in some kind of data structure that must fulfill some crucial conditions. We will explain them later but, first, let us establish and clarify the elements that configure our scenario.

Suppose we have a continuous sequence of records: access logs, event logs, transaction logs, or any sequenceable data of your choice. Such sequence can be materialized in one or multiple log files and therefore provide an audit trail to understand the activity of a system. And so, it may be subject to queries by users who want to diagnose problems. The evidence one seeks in these sorts of diagnostic investigations often takes the form of statements of existence and order. But this kind of tamper-evident logs have also been employed for other use cases like building versioned file systems, peer-to-peer protocols, or as a mechanism to detect inconsistencies between replicas in a distributed system.

We can identify three agents in our schema: a source or author, that generates data records and must be trusted by definition; a logger, that materializes and keeps the log; and one or multiple auditors.

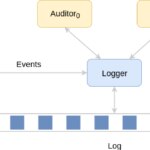
Given that we are assuming the logger is never trusted, and is free to lie when generating results in response to queries, tampering cannot be detected unless some trusted auditor—at least one—is auditing it. That situation leads us to emphasize the need for continuous auditing for correctness. Auditing must be therefore a frequent operation, and so, must be optimized in terms of performance.

But, how can an auditor fulfill its mission? We can see that the process of auditing involves two roles: prover and verifier. The logger plays the role of the prover. It stores data and answers queries about it. Along with the response to those queries, it returns a piece of information that acts as as a proof of validity of the answer. That proof can be efficiently checked by a verifier. The auditor plays the role of the verifier. It makes queries to the prover and verifies the results leveraging the proof.

To support this scenario, the logger needs to implement a special kind of data structure whose operations, in response to user queries, can be carried out by untrusted provers. Such data structure has been formalized in detail and given the name authenticated data structure (ADS) [2]. ADSs are, therefore, the main element we will explore in our intent to support moving data to untrusted servers without losing data integrity.

Basic building blocks

The problem of certificate revocation [3, 4] in public key infrastructure motivated early works on ADSs. Most of these works leverage two cryptographic primitives as building blocks to transform regular data structures into proper ADSs: cryptographic hash functions and digital signatures. Hash functions operate as secure compression mechanisms. They map a large space of possible records to a smaller space of digests. Collisions, although theoretically possible, are computationally hard to find. For their part, digital signatures provide authenticity, non-repudiation and integrity of records, supplying the signer with a mechanism to prevent forging while enabling verification by third parties.

Combining these two techniques, an untrusted logger could produce a stream of signed commitments in response to an input stream of events, generating a new signed commitment for each event added to the log. This is one of the first approaches to ADSs we can imagine: a hash chain where each commitment snapshots the entire log up to that point. This technique allows us to establish a provable order between entries and ensure that any commitment to a given state of the log is implicitly a commitment to all prior states. Therefore, any subsequent attempt to remove or alter some log entries will invalidate the hash chain.

In order to prove that an entry has been included in the chain and that it has not been modified in an inconsistent way, we have to produce three kinds of proof:

• Proof of inclusion, answering the question about whether a given entry is in the log or not.
• Proof of consistency, answering the question about whether a given entry is consistent with the prior ones. This ensures the recorded history has not been altered.
• Proof of deletion, so we are able to know when a log has been tampered with—deleted—at its source location.

Unfortunately, hash chains are not very efficient ADSs. They present linear space and time behaviour (O(n)) because they require that auditors to examine every intermediate event between snapshots for a simple membership query. While other data structures have been proposed to improve on the hash chains, e.g.: skip lists [5], research in certificate transparency focused on authenticated dictionaries, introducing a hash tree scheme based on the work of Ralph Merkle.

A hash tree or Merkle tree is a kind of binary tree that uses cryptographic hash functions and has a long history of uses implementing static authenticated data. In a Merkle tree, leaves store data records and compute their own hash. Parent nodes derive their hash computing a hash function on their children’s hashes concatenated left to right. The root hash is then a tamper-evident summary of all contents. We call this summary the commitment of that tree.

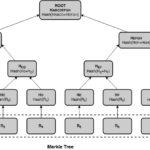
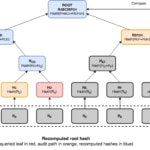
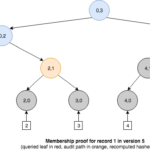
Merkle trees are very interesting data structures for our purposes. Since they store data only in the leaves they use linear space, and due to their being binary trees, the length of a path from the root to the leaves is logarithmic with the size of the tree. This property provides efficient random access to the leaves, but also allows constructing efficient membership proofs. Membership proofs request the logger to prove if a particular event exists in the tree and that it is consistent with the published commitment. These proofs include what are known as Merkle audit paths.

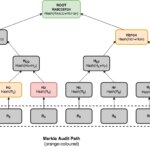
An audit path for a leaf is composed of all additional nodes required to compute the root hash for that tree. We can see that the minimum audit path includes one node for every layer of the tree, making the size of the proof O(log n). Given that an audit path is a kind of pruned tree, it also offers efficient query and verification times of O(log n). An audit path can be verified by recomputing all hashes, bottom-up, from the leaf towards the root node. Once we have a recomputed root hash, we can compare it with the original root hash of the Merkle tree—the commitment. If both match, then the proof is believed to be valid, provided that a trustworthy root hash is available for comparison. We could achieve this goal by combining hash trees with the use of digital signatures to sign the commitments by a trusted party.

Merkle tree drawbacks

While a plain hash tree has useful properties for implementing static authenticated dictionaries, it cannot satisfy those that arise when faced with a dynamic scenario. We can see that it efficiently supports query operations with their corresponding proof, but it requires rebuilding the entire tree on each update operation. Since every operation reads, and maybe updates, the root of the hash tree, concurrency gets limited and so, performance significantly reduced. Under concurrent update-heavy workloads this situation gets magnified.

Update scenarios show another important limitation of the hash tree: when we perform an update operation we are losing the required information to reconstruct past versions of that tree. When an ADS is able to capture its history of changes, we say it is persistent. This is a fundamental requirement when building a log, where data gets sequenced. In a log there exists a weak notion of time due to the ordering of record insertion: for any given entry, entries to its left are "older" than entries to its right. A hash chain can easily fulfill this ordering by its chained nature but, how can we achieve this requirement with a Merkle tree?

We have previously seen that a hash tree stores the records at the leaves but we haven’t said anything about the position the records occupy at the lowest level of the tree structure. If we fill the records left-to-right at that level, while keeping the insertion order, we could reproduce the behaviour of a log. A binary tree that behaves that way is called a complete binary tree. A binary tree is complete if all of its levels are completely filled except perhaps the last level, and in that lowest level, leaves are filled left-to-right.

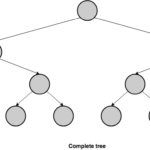
This combination of a Merkle tree and a complete tree is what Crosby and Wallach called a history tree [6].

History tree

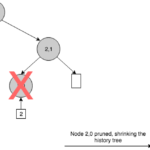
In essence, a history tree is a versioned Merkle tree where records are stored left-to-right at the lowest level, following an append-only model. Like a hash chain, this ADS is naturally persistent, with the difference that it supports efficient membership proofs. On every insertion, it generates a new Merkle tree with a possibly increasing number of levels and then, it computes a new root hash that works as a snapshot of the entire log at that point in the sequence. We can see that a history tree grows always from left to right. This growth property allows us to make efficient claims about the past because we can reconstruct old versions of the tree by pruning specific branches from right to left.

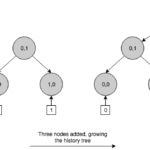
Nodes in a history tree are identified by an index and a layer (N_i,l). The index corresponds to a specific version of the tree. Since the leaves layer corresponds to layer 0, a leaf node is identified by the new version of the tree, produced when inserting the event associated to that leaf, and a layer of 0, i.e.: N_i,0. Interior nodes take their index from the index value of the last descendant to the left. For instance, a version 5 tree, has 6 events stored at the layer 0 (from 0 to 5) and a depth of 3. We can observe that this tree is not completely filled because a depth 3 tree can store a maximum of 2³ events on the leaves. If we exceed that number, the tree will grow in depth to 4, and so on and so forth.

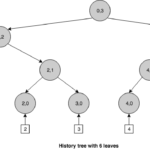
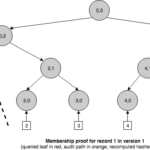
Unlike an ordinary Merkle tree, a history tree can produce membership proofs that allow to verify if a particular event is present in the log and is consistent with the current commitment, but also with commitments in the past. For example, we could prove that the event inserted in version 1 was consistent with version 1 but it is still present in version 5.

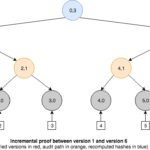
Besides membership queries, a history tree also enables us to generate a new type of proof called incremental proof, that can be used to show consistency between commitments for different versions of the tree. That is, all events in the earlier version are present in the newer one. To achieve this, the proof must return just enough information to reconstruct both root hashes so that they can be compared with the published commitments.

But not everything is perfect for our needs. We can observe that since a history tree stores event digests at the leaves, it does not allow to search for such digests efficiently by their contents, as they are sorted by their insertion time instead of lexicographically. This property is essential to construct what is called a binary search tree (BST). A BST requires the value of each node to be greater (or lesser) than the value of its left (or right) child, that is, it implies a lexicographical order that allows the lookup operations to use the divide-and-conquer technique known as binary search. As previously seen, every node is labeled with two values that conform a key: an index and a layer. This index can be used to navigate along the tree using the binary search algorithm, but it is insufficient to make a membership proof based only on the original event. We would need to avail of some mechanism able to map the hash of the original event to the version of such event in the history tree.

We can identify a similar problem with non-membership proofs. Even having a mapping mechanism between event digests and versions, there is no way to generate an audit path for events not present in the history tree. To accomplish this query, we would have to comb through the entire list of leaves to ensure a particular event does not exist in the tree. But it is obvious that such operation is as inefficient as the corresponding one in the hash chain.

So now we have to confront two fundamental challenges: how to map event digests to versions in the history tree in order to make membership proofs, and how to generate efficient non-membership proofs. In the next part of this series we will see how we managed to overcome these problems.

References

[1] QED,
https://github.com/BBVA/qed

[2] R. Tamassia. Authenticated data structures. In 11th Annual European Symposium on Algorithms, Sept. 2003,
https://cs.brown.edu/research/pubs/pdfs/2003/Tamassia-2003-ADS.pdf.

[3] Laurie, B., Kasper, E. Revocation transparency. Google Research (2012),
http://www.links.org/files/RevocationTransparency.pdf.

[4] Laurie, B., Langley, A., Kasper, E. Certificate Transparency. RFC 6962 (2013),
http://tools.ietf.org/html/rfc6962.

[5] Goodrich, M., Tamassia, R., and Schwerin, A. Implementation of an authenticated dictionary with skip lists and commutative hashing. In DARPA Information Survivability Conference & Exposition II (DISCEX II) (Anaheim, CA, June 2001), pp. 68–82.
https://cs.brown.edu/cgc/stms/papers/discex2001.pdf.

[6] Crosby, S.A., Wallach, D.S. Efficient Data Structures For Tamper-Evident Logging. In USENIX Security Symposium. pp. 317–334 (2009),
http://tamperevident.cs.rice.edu/papers/paper-treehist.pdf.